| 1. Motivation
Was sind
digitale Unterschriften und wozu werden sie benötigt?
Dieser Text möchte diese und ein paar andere Fragen,
die zum Verständnis der Materie dringend benötigt
werden, beantworten.
Es ist hilfreich sich zuerst Gedanken
zu machen, was man eigentlich mit einer herkömmlichen
Unterschrift bezweckt.
Eine Unterschrift belegt:
die Urheberschaft (Authentizität)
eines Dokuments
Durch die Unterschrift wird festgelegt, dass das Dokument
von dem Unterschreibenden selbst stammt.
die Unverfälschtheit (Integrität)
eines Dokuments
Ein schriftliches Dokument wird erst nach der Erstellung unterschrieben.
Durch die Unterschrift wird ausgedrückt, dass das Dokument,
so wie es vorliegt, vom Urheber stammt.
die Einmaligkeit eines Dokuments
Jedes Dokument wird separat unterschrieben. Damit wird die
Einmaligkeit eines Dokuments belegt. Die Unterschrift kann
nicht kopiert und für ein anderes Dokument verwendet
werden.
die Verbindlichkeit eines Dokuments
Der Unterschreibende kann nicht abstreiten, dass das Dokument
von ihm stammt.
Digitale Unterschriften sind für
den elektronischen Abschluss von rechtsgültigen Verträgen
nötig.
Nachfolgend einige Grundlagen, die
zum Verständnis benötigt werden.
2. Kommunikation ohne Verschlüsselung
Zwei Menschen/Computer kommunizieren
über einen Kanal miteinander. Die Kommunikation wird
nicht verschlüsselt. Deshalb kann ein Eindringling, der
den Kanal abhört, an die Daten kommen.

3. Kommunikation mit Verschlüsselung
Diese beiden Personen/Computer kommunizieren
über einen Kanal, diese Kommunikation findet allerdings
verschlüsselt statt. Der Eindringling kann zwar den Kanal
abhören, mit den Daten aber nichts anfangen. Hier ist
das Ziel der Verschlüsselung, Daten/ Informationen vor
nicht autorisierten Personen zu schützen.

4. Prinzip der Verschlüsselung
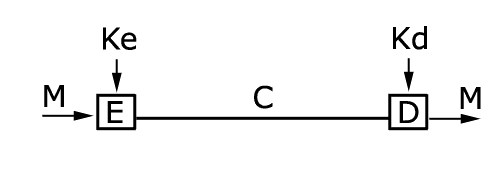
Sei
M = Nachricht
Ke = Schlüssel zur Verschlüsselung
Kd = Schlüssel zur Entschlüsselung
E = Chiffrieralgorithmus
D = Dechiffrieralgorithmus
C = Verschlüsselte Nachricht
Die verschlüsselte Nachricht
C erhält man, indem man die Nachricht M mit Hilfe des
Chiffrieralgorithmus E und des Schlüssels zur Verschlüsselung
Ke bearbeitet.
C = EKe (M)
Die ursprüngliche Nachricht M
erhält man, indem man die verschlüsselte Nachricht
C mit Hilfe des Dechiffrieralgorithmus D und des Schlüssels
zur Entschlüsselung Kd bearbeitet.
M = DKd (C)
D ist die Inverse zu E, weil folgendes
gilt: DKd (C) = DKd ( EKe (M) ) = M
5. Symmetrische Verschlüsselung (Private-Key-Verfahren)
Bei der symmetrischen Verschlüsselung
sind Ke und Kd identisch, d.h. für das Verschlüsseln
und Entschlüsseln wird der gleiche Schlüssel benutzt.
Dies erfordert, dass der Schlüssel der zweiten Person
zugänglich gemacht werden muss. Falls man mit mehr als
einer Personen verschlüsselte Kommunikation betreiben
möchte, so müssen diese ebenfalls im Besitz des
Schlüssels sein.

Beispiel:
B möchte mit A kommunizieren. Hierzu ist es nötig,
dass A seinen Schlüssel B zukommen lässt. B verschlüsselt
seine Nachrichten an A mit dem Schlüssel K von A. A kann
mit seinem Schlüssel K die Nachricht entschlüsseln.
Hier wird deutlich, dass der Schlüssel K nicht über
einen unverschlüsselten Kanal übertragen werden
darf.
Die Schlüsselverwaltung ist ein
Hauptproblem der symmetrischen Verschlüsselung. Als Schlüsselverwaltung
bezeichnet man das Erzeugen, Übertragen und das Speichern
von Schlüsseln.
Ein Beispiel für ein symmetrischen
Verfahren ist DES (Data Encryption Standard).
6. Asymmetrische Verschlüsselung (Public-Key-Verfahren)
Wenn unterschiedliche Schlüssel
Ke und Kd benutzt werden, so spricht man von asymmetrischer
Verschlüsselung. Kd und Ke weisen gleichartige Eigenschaften
auf. Dies bedeutet, dass die mit einem Schlüssel verschlüsselte
Nachricht nur mit dem zugehörigen zweiten Schlüssel
entschlüsselt werden kann.

Beispiel:
B möchte mit A kommunizieren. A hat zwei Schlüssel,
nämlich einen privaten Kpriv und eine öffentlichen
Schlüssel Kpub. Den privaten Schlüssel behält
A bei sich, den öffentlichen Schlüssel veröffentlicht
A oder kann ihn an B schicken, dies sogar im Klartext über
einen unverschlüsselten Kanal. B verschlüsselt mit
dem öffentlichen Schlüssel von A die Nachricht an
A. Nur A ist mit seinem privaten Schlüssel in der Lage
die Nachricht zu entschlüsseln.
Ein Beispiel für ein asymmetrisches
Verfahren ist RSA.
7. Hash Verfahren bzw. Hash Algorithmus
Ein Hash Algorithmus H bildet eine
beliebige lange Binärfolge B auf eine eindeutigen Hashwert
F ab. F wird auch als Fingerabdruck (engl. : Digital Fingerprint)
bezeichnet.
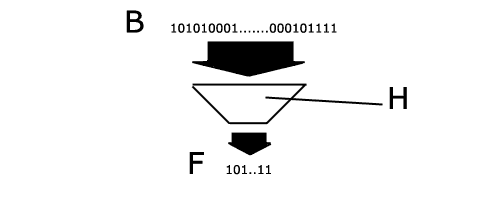
Der Hash Algorithmus muss eine Einweg-Funktion
sein, d.h. es darf von dem Hashwert F nicht auf die Eingabe
B geschlossen werden.
H muss immer den selben Hashwert F
liefern. Falls auch nur ein Bit der Binärfolge geändert
wird, so muss H einen komplett anderen Hashwert F liefern.
Deshalb muss der Hash Algorithmus so konstruiert sein, dass
sämtliche Bits der Binärfolge B in den Hashwert
F einfliessen.
Die Wahrscheinlichkeit, dass zwei
unterschiedliche B den selben Hashwert F liefert, sollte so
niedrig wie möglich sein. Falls unterschiedliche B das
selbe F liefern, so spricht man von einer Kollision. Ganz
vermeiden lässt sich das natürlich nicht, weil der
Hash Algorithmus immer eine "Verdichtung" darstellt.
Falls ein Hash Algorithmus z.B. einen 16-Bit Hashwert F liefert,
so liegt die Wahrscheinlichkeit bei 1 zu 65000, dass es zu
einer Kollision kommt. Wählt man allerdings einen 128-Bit
Hashwert, so kann man relativ sicher sein, dass es zu keiner
Kollision kommt.
Der Hash Algorithmus MD5 liefert z.B.
aus einer beliebigen Binärfolge einen 128-Bit Hashwert.
8. Digitale Unterschriften mit symmetrischer Verschlüsselung
A möchte an B ein digital signiertes
Dokument zusenden. Es sind folgende Schritte notwendig.
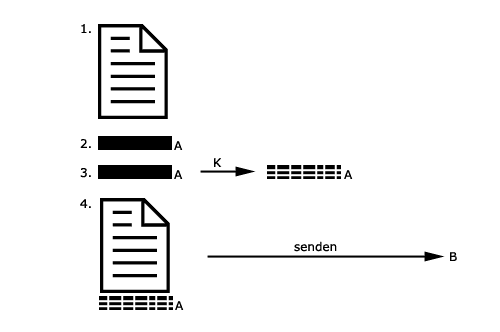
1. Das Dokument wird erstellt.
2. Berechnung des Hashwertes für das zu signierende Dokument.
3. Verschlüsselung des Hashwertes mit dem Schlüssel
K.
4. Der Hashwert wird dem Dokument angefügt und an Empfänger
B gesendet.
B empfängt das signierte Dokument. Bei B sind folgende
Schritte notwendig.
1. Das Dokument mit dem angehängten
Hashwert wird empfangen.
2. Trennen von Hashwert und Dokument
3. B berechnet mit dem gleichen Algorithmus einen Hashwert
des Dokuments.
4. Der verschlüsselte Hashwert des Dokuments wird mit
dem Schlüssel K enschlüsselt.
5. B vergleicht den selbst errechneten Hashwert mit dem entschlüsselten
Hashwert von A.
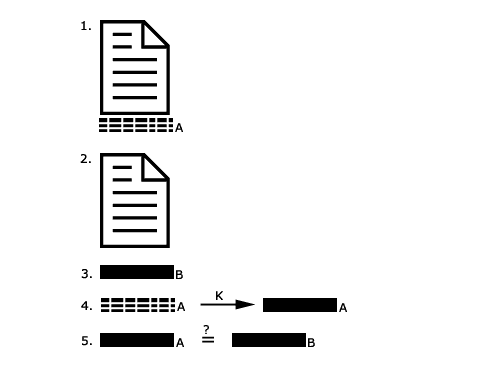
Falls das Dokument unterwegs von (A zu B) manipuliert wurde,
so kann B das herausfinden. Beim Vergleich der Hashwerte merkt
B, dass das Dokument verändert wurde. Die Hashwerte wären
nicht identisch. Die Unverfälschtheit (Integrität)
eines signierten Dokumentes kann also mit der symmetrischen
Verschlüsselung geprüft werden.
Wie sieht es mit der Urheberschaft (Authentizität) eines
Dokuments aus? Kann B gegenüber einem unabhängigen
Dritten beweisen, dass A der Urherber des signierten Dokuments
ist? Nein, da B selbst in Besitz des Schlüssels K ist,
könnte B selbst den Hashwert bilden und ihn mit dem Schlüssel
K verschlüsseln. Sämtliche Schritte, die A gemacht
hat, können von B ebenfalls gemacht werden.
9. Digitale Unterschriften mit asymmetrischer Verschlüsselung
A möchte an B ein digital signiertes
Dokument zusenden. Es sind folgende Schritte notwendig.
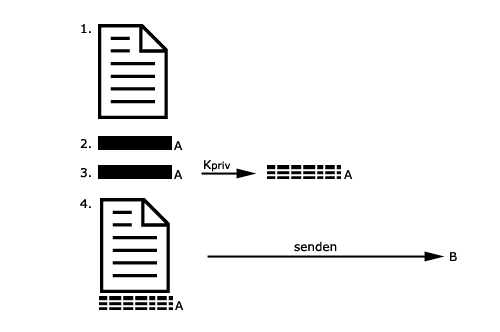
1. Das Dokument wird erstellt.
2. Berechnung des Hashwertes für das zu signierende Dokument.
3. Verschlüsselung des Hashwertes mit dem privaten Schlüssel
Kpriv.
4. Der Hashwert wird dem Dokument angefügt und an Empfänger
B gesendet.
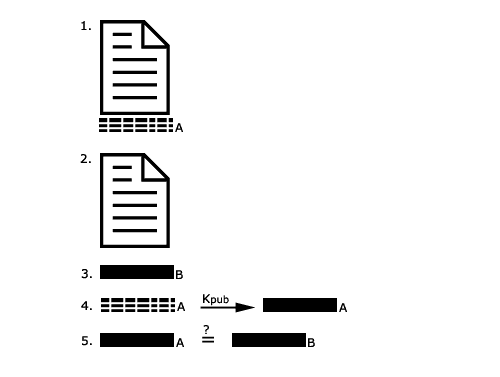
1. Das Dokument mit dem angehängten
Hashwert wird empfangen.
2. Trennen von Hashwert und Dokument
3. B berechnet mit dem gleichen Algorithmus einen Hashwert
des Dokuments.
4. Der verschlüsselte Hashwert des Dokuments wird mit
dem öffentlichen Schlüssel Kpub von A entschlüsselt.
5. B vergleicht den selbst errechneten Hashwert mit dem entschlüsselten
Hashwert von A.
Falls das Dokument unterwegs von (A
zu B) manipuliert wurde, so kann das festgestellt werden.
Beim Vergleich der Hashwerte merkt B, dass das Dokument verändert
wurde. Die Unverfälschtheit (Integrität) eines signierten
Dokumentes kann mit der asymmetrischen Verschlüsselung
geprüft werden.
Auch die Urheberschaft (Authentizität) des Dokuments
kann gegenüber einem Dritten nachgewiesen werden. Denn
nur A, der in Kenntnis seines privaten Schlüssels Kpriv
ist, kann den Hashwert verschlüsselt haben. Falls mit
Kpub der Hashwert entschlüsselt werden kann, ist das
ein Nachweis der Urheberschaft von A. B kann keinen Hashwert
erzeugen und mit dem Schlüssel Kpub verschlüsseln,
denn er lässt sich mit dem Kpub nicht öffnen. Nur
das, was mit Kpub verschlüsselt wurde lässt sich
mit Kpriv öffnen und umgekehrt.
|